Qué es un ataque Padding Oracle y cómo funciona

Share this on → [Mastodon] [Twitter] [Facebook]

Comencemos con una demostración. El siguiente video muestra cómo un programa ejecutando en mi portátil es capaz de descifrar un mensaje cifrado con AES-256 en modo CBC y padding PKCS7.

Recordemos que AES es seguro. El tiempo para romper por fuerza bruta una clave AES-256 en un supercomputador actual es de aproximadamente 10⁵² años. Con 1000000000 GPUs de 2 Gigaflops, 60²⁵ años. Además, necesitarías 150 Gigavatios para alimentarlas, esto es, 150 reactores nucleares.

En esta demostración, tanto el cliente como el servidor son correctos: no tienen bugs explotables, usan correctamente las herramientas criptográficas, etc.

Ahora mira:

Ok. El único fallo que tiene el servidor es el siguiente: cuando hay un error en el mensaje, hace visible al cliente si se trata de un error en el padding del mensaje o no. Simplemente eso.

Un ataque de oráculo es un ataque de side-channel. En general, un ataque de oráculo es cuando el protocolo o sistema tiene un canal lateral que permite deducir si ocurre o no ocurre una cosa, permitiendo al adversario saber si está cerca o no de conseguir un objetivo.

En este caso, el side-channel consiste en saber si un mensaje cifrado que envía el atacante tiene bien formado el padding o no.

Esto lo puede saber si el servidor devuelve un error que permite diferenciar si hay un error de padding o si el error es de otro tipo. También se podría saber midiendo el tiempo que tarda el servidor en responder a una petición, etc.

El atacante puede sacar partido de esto para descifrar cualquier mensaje sin tener la clave AES de 256 bits. Esto se hace explotando un efecto del modo de operación CBC, que vemos a continuación.

CBC

AES es un cifrador de bloques, funciona así:

Crifrador de bloques

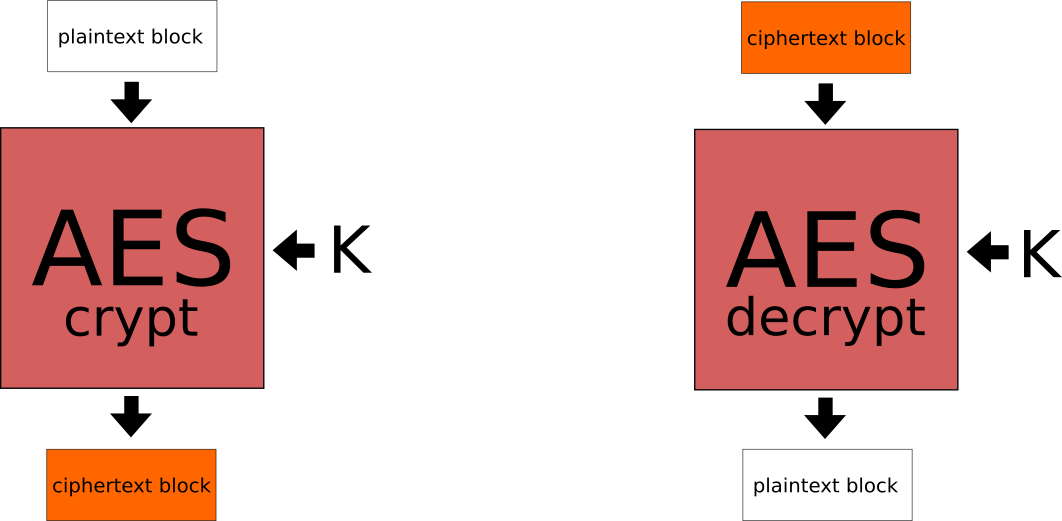
Cuando queremos usar un cifrador de bloques como AES para cifrar una mensaje en claro (M a partir de ahora) más largo que un bloque (128 bits en el caso de AES), necesitamos usar un modo de operación. Hasta hace poco, el modo de operación estándar era CBC. En la actualidad se recomiendan otros modos, pero CBC sigue en uso y no se considera inseguro (siempre que se tomen precauciones).

Para cifrar un mensaje largo, se parte en trozos del tamaño de bloque del algoritmo (128 bits en AES/Rijndael). Cada trozo se cifra con AES usando la clave indicada. El modo de operación establece cómo se cifran los distintos trozos.

Si se cifran todos los bloques tal cual (modo llamado ECB), los bloques del mensaje cifrado (C a partir de ahora) pueden terminar con patrones derivados del mensaje en claro. Piensa en esto: si estás cifrando un pixmap y tienes la mala suerte de que cada pixel ocupa un bloque completo, el pixmap cifrado será otro pixmap en el que unos colores se han reemplazado por otros. Seguramente puedas reconocer la imagen cifrada.

El modo CBC se pensó para evitar ese efecto y ocultar patrones del mensaje en claro. Este modo consiste en hacer una operación XOR bit a bit entre el bloque N del mensaje en claro y el bloque N-1 del mensaje cifrado, antes de pasarlo por el cifrador AES. De esta forma, se están encadenando los bloques. Al resultado de ese XOR (esto es, el bloque antes de pasar por el cifrador) se le llama estado intermedio. Esto es importante, aparecerá más tarde.

Por tanto, en CBC un bloque i se cifra así (siendo K la clave):

C[i] = AES_K(M[i] ⊕ C[i-1])

Descifrado en el modo CBC.

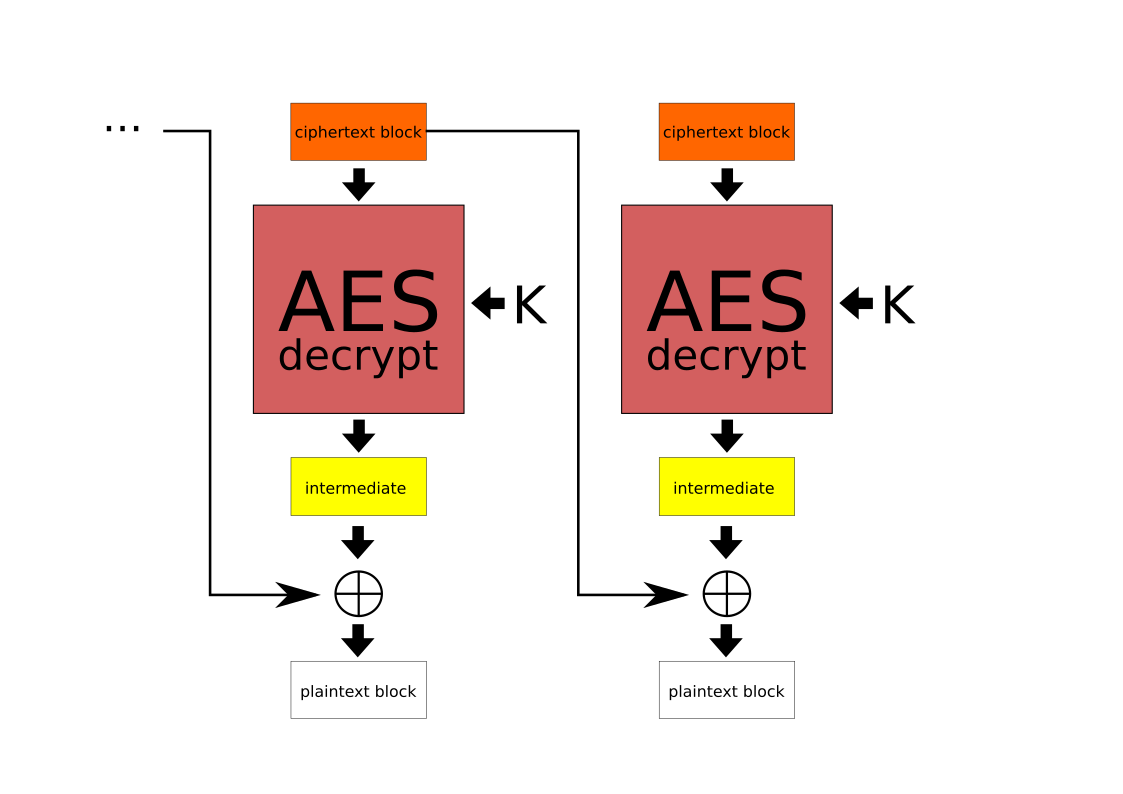
Para el primer bloque del mensaje, que no tiene anterior, se usa el vector de inicialización, que se debe proporcionar junto con la clave a la hora de cifrar/descifrar el mensaje con AES en modo CBC (y debe ser aleatorio, no predecible y no se debe reusar).

Un problema importante del modo CBC es que es maleable. Esto significa que el atacante puede modificar el mensaje cifrado para provocar cambios en el mensaje descifrado.

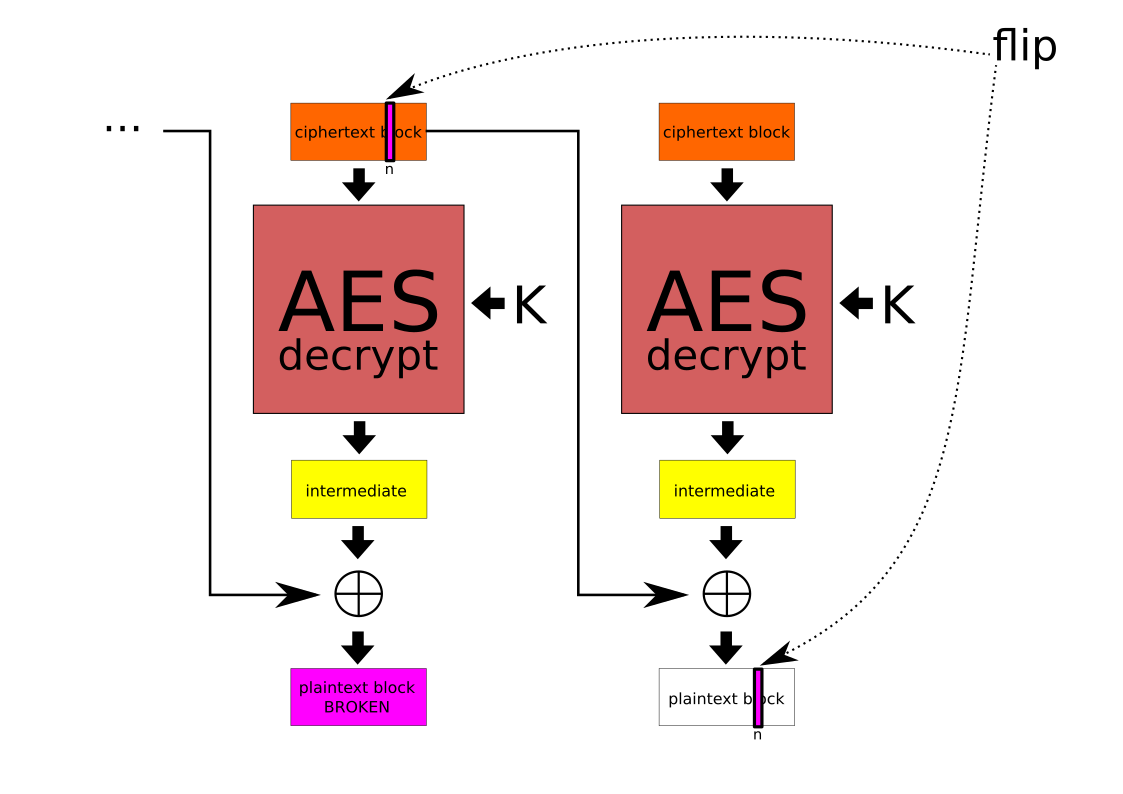
En CBC, el cambio del bit i del bloque N del mensaje cifrado supone dos cambios en el mensaje descifrado:

1. El bloque N del mensaje descifrado cambiará completamente (no tendrá ningún sentido).
2. Se provoca un flip del bit i del bloque N+1 del mensaje descifrado: ese bit habrá cambiado (será 0 si antes era 1, y viceversa).

Mucha gente piensa que una modificación en un mensaje cifrado en modo CBC destroza el mensaje descifrado desde el bloque modificado hasta el final del mensaje. No es así. El bloque N+2, y los siguientes, no se ven afectados por esa modificación del mensaje cifrado.

Modificación de un bit del texto cifrado en modo CBC.

Padding

Cuando tenemos un mensaje que no es múltiplo del tamaño del bloque, el último bloque del mensaje se tiene que rellenar, ya que al cifrador hay que darle bloques completos.

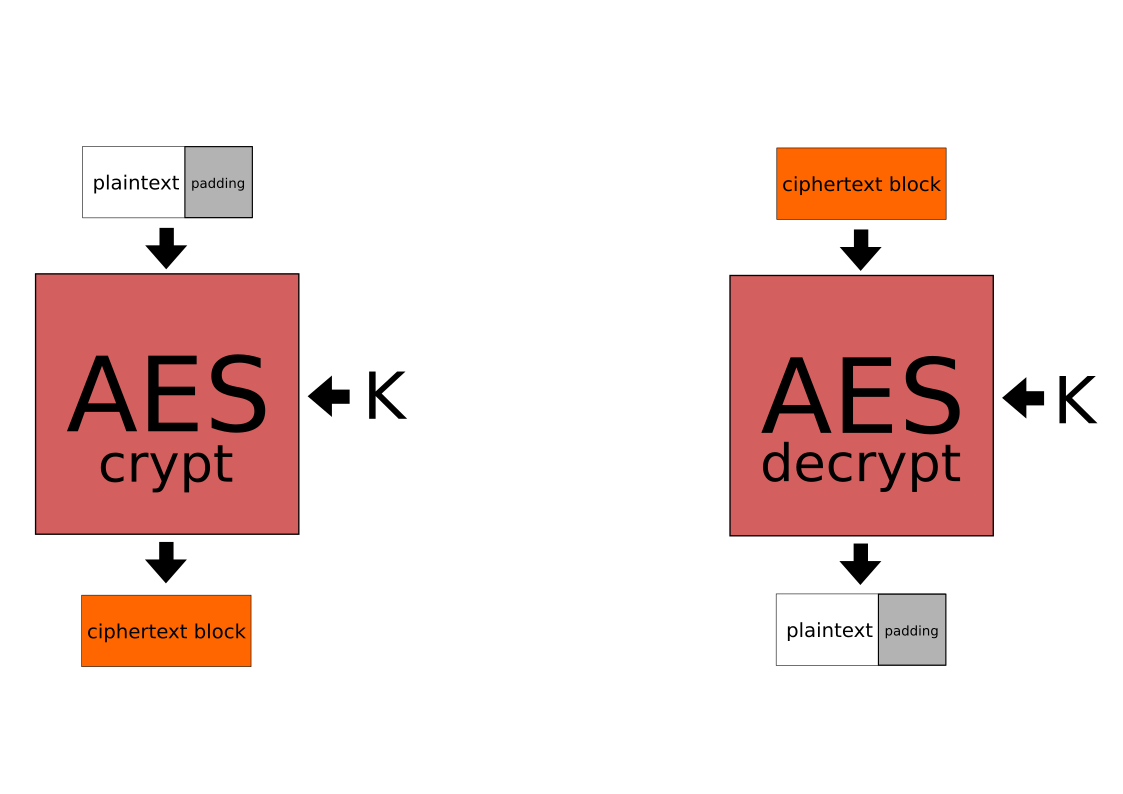
Hay varias formas de hacer esto. Para este ejemplo estamos usando el estándar de padding PKCS7, que consiste en rellenar con todos los bytes puestos al número de bytes del padding:

      01
      02 02
      03 03 03
      04 04 04 04
      05 05 05 05 05
      etc.

Por ejemplo, si en el último bloque tienes que rellenar con 7 bytes, se pondrían los siete con un valor 0x07. Si el mensaje es múltiplo del tamaño de bloque, se debe meter un bloque completo de padding.

Ataque

Para realizar el ataque, el adversario necesita:

1. Capturar el tráfico cifrado legítimo de un cliente.

2. Poder enviar peticiones espurias al servidor.

3. Diferenciar los fallos provocados por un padding incorrecto del resto de fallos. Esta es la fuga de información necesaria para realizar este ataque de side-channel.

Ataque I: conocer el tamaño del mensaje cifrado

El primer ataque, más sencillo, consiste en descubrir el tamaño del mensaje cifrado (esto es, saber cuánto padding se ha usado). Esto es algo que un atacante no debería poder descubrir.

Para ello:

1. Se envían versiones modificadas del mensaje cifrado original, C.

2. Por cada intento, se modifica un único byte del penúltimo bloque de C.

3. Se empieza modificando el último byte de ese bloque, y se va iterando hacia atrás.

4. Paramos cuando el servidor no de un error de padding (dará otro tipo de error).

5. Si eso pasa en N-ésimo byte del penúltimo bloque, ya sabemos que el mensaje original tiene una longitud en bytes de (siendo NBLOCKS el número total de bloques del mensaje cifrado C):

LEN(M) = BLOCKSIZE * (NBLOCKS - 1) + N

Ataque II: descifrar un mensaje interceptado previamente

Ahora el objetivo es descifrar un mensaje de un cliente legítimo capturado previamente, que mucho más interesante.

Llamemos C[i] al bloque del mensaje cifrado C que queremos descifrar. La idea principal es esta:

1. Usaremos C[i] como último bloque de un mensaje espurio que llamaremos fake. Esto es, se usará como el bloque en el que tendría que estar el padding.

2. Modificaremos repetidamente el penúltimo bloque del mensaje espurio, fake[j], para descubrir cuándo el servidor no retorna un error de padding. Cuando no retorne error de padding, paramos.

3. Ya tenemos el valor intermedio de cada byte de C[i].

4. Con el valor intermedio, reconstruiremos cada byte del correspondiente bloque del mensaje en claro original, M[i].

5. Esto lo haremos por cada bloque de C hasta conseguir el mensaje en claro original completo, M.

Veamos cómo descifrar un único byte del último bloque del mensaje en claro (el bloque de la posición last).

Así encontramos el valor val que hace que el último byte al descifrar C[i] sea 0x01, que hace que sea un padding PKCS7 correcto de 1 byte (y en ese caso el servidor devolverá un error distinto a padding incorrecto):

val := 0
found := false
while val <=  255 and not found
    fake[j][last] := val
    sendFakeMessage()
    if not paddingError then
         found := true
    else
         val := val + 1
    end if
end while

Obtenemos el valor intermedio correspondiente a dicho byte:

I := val ⊕ 0x01

Después obtenemos el valor del byte en el texto claro, M[i][last], usando el bloque cifrado anterior del mensaje original, C[i-1][last]:

M[i][last] := C[i-1][last] ⊕ I

Después, para descifrar el penúltimo byte, C[i][last-1]:

1. Hacemos lo mismo, pero teniendo en cuenta que el padding correcto ahora debe ser 0x02,0x02.

2. No hay problema, dado que ya sabemos el valor de M[i][last].

3. Podemos calcular el valor de fake[j][last] para que al descifrar el último byte del mensaje espurio descifrado sea 0x02.

Y así con el resto de bytes del bloque i.

Para descifrar el primer bloque C[0], debemos usar el vector de inicialización.

La esperanza es descifrar el mensaje entero en 128 * len(M) peticiones al servidor.

Implementación del ejemplo

Puedes encontrar el código de la demostración implementado en Go en este gitlab:

https://gitlab.etsit.urjc.es/esoriano/padding-oracle

Puedes bajarlo así:

$> go get -d -v gitlab.etsit.urjc.es/esoriano/padding-oracle.git

Y para ejecutarlo:

$> cd $GOPATH/src/gitlab.etsit.urjc.es/esoriano/padding-oracle.git
$> go run server.go &
$> go run client.go
$> go run attack.go

Contramedidas

Para evitar este tipo de ataques, podemos implementar ciertas contramedidas:

1. Usar un modo de operación no maleable o un modo de operación autenticado (p. ej. GCM).

2. No dar detalles a los clientes sobre los errores internos del servidor que tienen que ver con la seguridad.

3. Intentar responder en un tiempo constante, independientemente del error que se produzca (evitar timing side-channels). Existen bibliotecas con operaciones con tiempo constante para diferentes operaciones (p. ej. subtle en Golang).

4. Limitar el número de peticiones inválidas de los clientes (espera exponencial, listas negras de clientes, etc.).

Historia

Este ataque fue publicado en 2002 por Serge Vaudenay [1], y se encontraron vulnerabilidades en JavaServer Faces, Ruby on Rails, ASP.NET, Steam y otros.

En 2013, se descubrió que OpenSSL y GnuTLS eran vulnerables a una variante llamada Lucky Thirteen [2]. OpenSSL no fue parcheado hasta 2016.

En 2014, se descubrió que TLS era vulnerable a una variante llamada POODLE (Padding Oracle On Downgraded Legacy Encryption) [3].

“Attacks only get better, they never get worse”, Bruce Schneier.

“Attack names do get worse”, Matthew Green.

Referencias

[1] Serge Vaudenay. Security Flaws Induced by CBC Padding Applications to SSL, IPSEC, WTLS. EUROCRYPT 2002.

[2] Nadhem J. AlFardan and Kenneth G. Paterson. “Lucky Thirteen: Breaking the TLS and DTLS Record Protocols”. Royal Holloway, University of London. Retrieved 21 June 2013.

[3] Matthew Green. “Attack of the week: POODLE”. Link.

_{^{(cc) Enrique Soriano-Salvador Algunos derechos reservados. Este trabajo se entrega bajo la licencia Creative Commons Reconocimiento - NoComercial - SinObraDerivada (by-nc-nd). Creative Commons, 559 Nathan Abbott Way, Stanford, California 94305, USA.}}